Tendinite e slalom gigante
Pochi giorni fa mi è comparso un fastidioso dolore al tendine d’Achille, probabile conseguenza di un leggero sovraccarico meccanico tra allenamenti di corsa e bici.
Poco male, mi sono detto, mi rinchiuderò in palestra a fare stretching per qualche giorno. Ma mentre tornavo a casa di pessimo umore, fantasticando su quando potrò tornare a correre, mi è tornato in mente l'indovinello con cui Luca Dellanna inizia il suo libro "Ergodicity".
Mio cugino è uno sciatore molto forte e partecipa al campionati mondiale di slalom gigante.
Durante ogni discesa ha il 20% di possibilità di cadere e rompersi la gamba ma, una volta arrivato al traguardo, ha il 20% di possibilità di vincere sui suoi avversari.
Quante gare si aspetta di vincere?
La risposta più immediata: 2 (il 20% di vittoria su 10 gare).
La risposta corretta: circa 0.71 .
Il motivo è facilmente intuibile dalla tabella riportata in seguito (crediti all’autore Luca Dell’Anna), mentre la dimostrazione matematica è riportata in fondo all’articolo.
| Gara | Prob. di partecipare | Prob. di arrivare in fondo | Vittorie attese |
|---|---|---|---|
| 1 | 100% | 80% | 16% |
| 2 | 80% | 64% | 13% |
| 3 | 64% | 51% | 10% |
| 4 | 51% | 41% | 8% |
| 5 | 41% | 33% | 7% |
| 6 | 33% | 26% | 5% |
| 7 | 26% | 21% | 4% |
| 8 | 21% | 17% | 3% |
| 9 | 17% | 13% | 3% |
| 10 | 13% | 11% | 2% |
| Totale | 0.71 |
Questa storiella mi serve a introdurre il concetto centrale di questo articolo: in teoria, la performance determina il successo: vince lo sciatore migliore in assoluto. In pratica, la sopravvivenza è condizione necessaria per la performance: vince lo sciatore migliore tra tutti i quelli in grado di gareggiare.

Fortunatamente, da piccolo sono sopravvisuto a gambe rotte e tendiniti.
Prometto che sono gli unici integrali di oggi
Tornando al mio infortunio, il principio di fondo è molto simile. Assumendo infatti, per economia della trattazione, che un infortunio sia irreversibile (una volta fatto il danno, non posso più curarmi e recuperare), la mia capacità di correre può essere rappresentata come una catena di Markov assorbente con due stati:
- Stato 1 (Transitorio): sto bene e sono in grado di correre.
- Stato 0 (Assorbente):sono infortunato.
Ogni giorno che mi alleno ho probabilità di rimanere nello stato 1 e una probabilità di infortunarmi e passare allo stato 0. Una volta raggiunto lo stato 0, ci resto per sempre.
Quanto appena descritto rappresenta perfettamente, esattamente come la vicenda del cugino, un processo non ergodico.
Ora allontaniamoci un attimo dalla mia tendinite e cerchiamo di definire meglio il concetto di ergodicità, per farlo, tuttavia, occorre prima definire due concetti.
- La media temporale è ciò che si ottiene osservando un singolo processo per molto tempo (es. una persona che pratica ripetutamente uno stesso gioco).
- La media spaziale (o d'insieme) è ciò che si ottiene osservando tante copie del processo in un solo istante (es. 100 persone che praticano lo stesso gioco contemporaneamente).
In formule, un processo è ergodico se:
Definizioni alternative sono proposte nell’appendice.
Dentro il casinò
Per chiarire il punto, serviamoci dell’ampliamente inflazionato esempio del casinò.
La Roulette Classica, in cui si punta su rosso o nero con pari probabilità di vincere (ignorando lo zero per semplicità) è un gioco ergodico.
Una persona che gioca 100 volte consecutive (media temporale), si aspetta di vincere circa 50 volte. Allo stesso modo da 100 persone che girano la roulette contemporaneamente (media spaziale), ci aspettiamo circa 50 persone soddisfatte della vincita. I tuoi risultati coincidono.
La Roulette Russa al contrario, in cui ci si punta in fronte un revolver con un proiettile su sei camere, non è un gioco ergodico.
Se una persona gioca consecutivamente 100 volte, nonostante inizialmente abbia una probabilità di sopravvivenza di 5/6, al primo clic sbagliato ci rimane secco (tasso di sopravvivenza nullo).
Se 100 persone giocano una volta, ci aspettiamo invece che circa 83 persone (5/6 di 100) sopravvivano (tasso di sopravvivenza pari, appunto, a 83%).
Dal momento che 0% 83%, concludiamo che la roulette russa è un processo non ergodico.

L'unica foto che ho all'interno di un casino (Montecarlo) | La cosa più vicina al gioco d'azzardo che conosco: giocare a scopone con gli amici.
L'infinito lasciamolo a Leopardi
Allontanandoci da questi due esempi estremi, si nota subito come l’ergodicità non sia un valore costante, bensì cambi in base all’orizzonte temporale su cui la valutiamo e, tendenzialmente, all’aumentare di , diminuisce anche l’ergodicità di un fenomeno.
Di conseguenza, dal momento che prendiamo decisioni su orizzonti temporali finiti e più o meno vicini a noi (lasciamo a matematici e filosofi il limite per ), possiamo collocare ogni azione su uno spettro di ergodicità, in base a quanto siano reversibili o meno i rischi sull’orizzonte considerato.
Se considerassimo un sufficientemente lungo, infatti, qualsiasi processo diventerebbe non ergodico: basti pensare al fatto che, adottando una visione della vita apocalittica, ogni azione che facciamo include una minima possibilità di rimanerci secchi e, di conseguenza, di non poter ripetere un esperimento all’infinito.
(Una delle poche attività quasi ergodiche che mi viene in mente è il lancio di dati in una stanza isolata priva di interventi esterni: a meno di morte improvvisa, si potrebbe andare avanti a gettare i dadi molto a lungo).
Non c’è più religione: tutte le chiese sono assicurate contro gli incendi
Lo studio dell’ergodicità introduce il concetto di irreversibilità e, di conseguenza, mi viene spontaneo ampliare la discussione di oggi a un concetto strettamente collegato: la gestione dell’incertezza.
Per fare ciò, distinguiamo i rischi in base a due proprietà: la reversibilità e l’assicurabilità.
- Un rischio è reversibile se, in un tempo finito e ragionevole, si può rimediare la perdita. Un rischio è irreversibile se le conseguenze sono abbastanza drastiche da rendere la perdita rilevante nel lungo periodo o tale da rendere il recupero sconveniente.
- Un rischio è gestibile se è possibile comprare un’assicurazione che ci rimborsi in caso di perdita, ingestibile altrimenti.
Per fare chiarezza, in seguito è riportata una tabella con degli esempi.
Anche in questo caso, non trattandosi sempre di proprietà binarie, sarebbe più corretto costruire un piano cartesiano in cui i due assi rappresentano queste due proprietà come variabili continue:
- asse - Gestibilità : meno infinito rappresenta il rischio totalmente ingestibile (un rimpianto di vita, una guerra nucleare), e l’estremo opposto il rischio totalmente assicurabile (come un piccolo danno coperto al 100% da polizza).
- asse - Reversibilità : meno infinito rappresenta il rischio totalmente irreversibile (la morte, in estremis), l’estremo superiore un rischio totalmente reversibile (perdere la metro prima tornando verso casa).
Di conseguenza, invece di collocarlo in uno dei quattro quadranti sopra riportati, ogni fenomeno della nostra vita diventa un punto sul piano del rischio.
Secondo quanto detto prima inoltre, i processi non ergodici sono il dominio dei rischi irreversibili (Quadranti 3 e 4) o, egualmente, tutti i punti con .
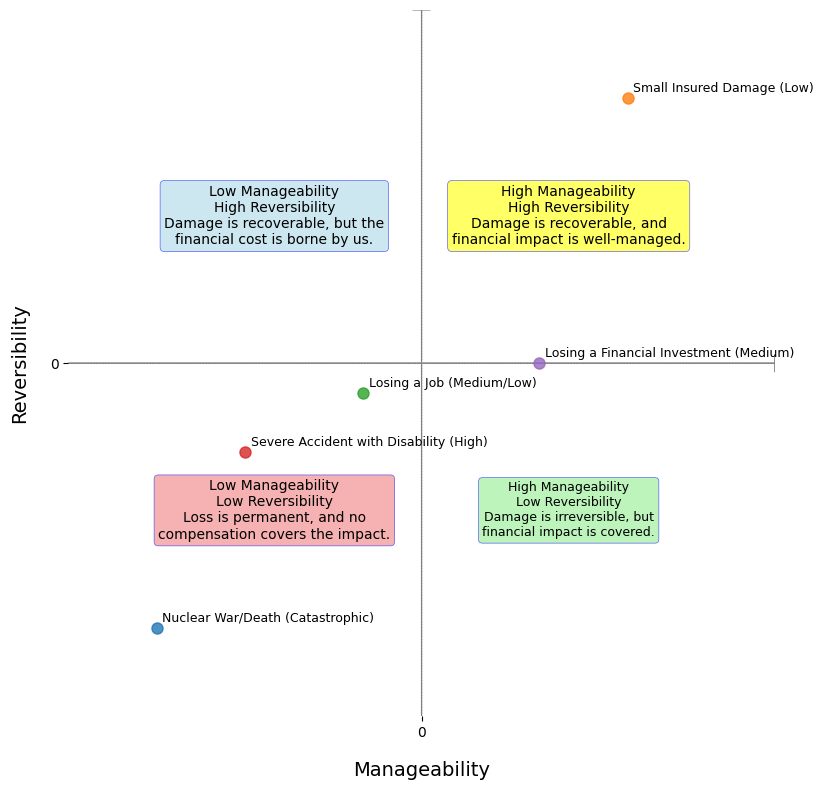
Esercizio di stile: provare a collocare ogni fonte di incertezza della vostra vita su questo grafico.
Fate stretching e tenete soldi liquidi
Dopo aver brevemente classificato l’incertezza, sorge spontanea la domanda su come gestire, abbracciare ed evitare le diverse tipologie di rischio.
Per rispondere a ciò, richiamiamo il tendine.
Una preparazione atletica ottimale non dovrebbe massimizzare i benefici di ogni singolo allenamento, bensì minimizzare il rischio irreversibile e ingestibile (Quadrante 3) di una tendinite (sostituite pure tendinite con qualsiasi altro infortunio sportivo) o, in altri termini, massimizzare la probabilità di essere ancora in grado di allenarsi nel lungo periodo.
Questo comportamento, anche chiamato principio di ridondanza, ci porta ad agire in modo apparentemente sub-ottimale nel breve termine, accentando risultati inferiori, per tuttavia massimizzare la sopravvivenza futura.
Nello sport, significa dedicare tempo allo stretching (apparentemente "inutile" e terribilmente noioso), prendere un giorno di riposo in più e non tirare ogni sessione al limite.
Nella finanza personale, significa mantenere un fondo liquido di emergenza (con rendimento nullo), accettando di abbassare il rendimento medio del portafoglio, ma proteggendosi dal rischio di rovina (insolvenza).
L’obiettivo del principio di ridondanza è quindi, dopo aver classificato ogni fenomeno come un punto sul piano, neutralizzare i rischi che non siamo disposti a prenderci , a prescindere da quanto sia infinitesimale la probabilità a essa associata.
Per approfondire meglio il prossimo argomento, ci tocca però tirare in mezzo chirurgi e sport estremi.

Avere del cibo in dispensa come semplice applicazione del Principio di ridondanza
Bungee Jumping, chirurgi e Skin in The Game
Il bungee jumping ha storicamente causato morto ogni salti. Un tasso bassissimo. Il problema è che a quel povero disperato a cui si rompe la fune, della statistica non importa nulla: su di lui si riversa il 100% della sfortuna in modo irreversibile.
Lo stesso vale per la chirurgia. Crediamo nella medicina moderna perché, in media, salva vite. Ma nel momento in cui il chirurgo sbaglia un'operazione, il paziente non si consola pensando a quanti sorrisoni guariti escono dall’ospedale ogni giorno.
Questi due esempi, appositamente estremi, servono a chiarire una lezione importante: in presenza di fenomeni non ergodici (o, in altri termini, di fronte a rischi irreversibili), il concetto stesso di probabilità classica e di media aritmetica perdono di significato per il singolo.
Quando un individuo affronta una perdita irreversibile e ingestibile a causa di un evento , la sua utilità (felicità) individuale è irrimediabilmente compromessa. Questo è vero a prescindere dal fatto che, in media, l'evento aumenti l'utilità (felicità) della popolazione. Trattandosi di una perdita senza possibilità di recupero e senza assicurazione, il beneficio medio goduto dagli altri diventa per lui irrilevante.
Generalizzando, si potrebbe inoltre concludere che la sopravvivenza di un sistema raramente coincide con la sopravvivenza dei suoi individui e che, spesso, il sistema non ha un incentivo sulla sopravvivenza dei suo membri. Al contrario, la sostituibilità dei singoli individui rende il sistema ergodico, antifragile o in grado di evolversi (a seconda dell’autore che leggete: Dell’Anna, Taleb o Darwin).
Il discorso cambia radicalmente se la perdita è gestibile. In tal caso, meccanismi di condivisione o trasferimento del rischio (p2p, polizze assicurative) possono proteggere l'individuo, permettendogli di beneficiare comunque di un potenziale aumento della propria utilità.
L’esempio del chirurgo, inoltre, mette in luce il il problema della "pelle in gioco" (skin in the game, come lo definisce Taleb). In molte situazioni l'entità che prende la decisione (esempio: un politico) non coincide con l’entità su cui ricadono le conseguenze negative irreversibili (esempio: i cittadini di un paese). Per il sistema ospedaliero, un decesso causato da errori evitabili è un numero su milioni di pazienti (situazione ergodica). Per lo sfortunato paziente, al contrario, è un evento di rovina al 100% (fenomeno non ergodico).
La soluzione a questo problema di diseallineamento suggerisce di agire in contesti in cui chi prende decisioni (amici, politici, aziende ecc ecc) coincide con chi paga le conseguenze di scelte sbagliate ma, per ovvie dinamiche del mondo reale, tale comportamento non è quasi mai possibile.

Politici (ed elettori) spesso non hanno skin in the game, i pizzaioli si: offrire una pizza scadente al cliente influenza negativamente i loro profitti.
Guardate sempre in alto mentre camminate per strada
Tutta la trattazione sul rischio, se condotta all’estremo, indurrebbe anche a non uscire più di casa per la paura che un vaso di ceramica ci caschi in testa. La verità è che il nostro cervello compie costantemente un'analisi costi-benefici valutando, in modo più o meno razionale, probabilità, benefici e utilità di ogni situazione a cui ci esponiamo esponiamo.
In linea di massima e del tutto teorica, la nostra avversione al rischio dovrebbe essere:
- Infinita per i rischi del Quadrante 3 (irreversibili e non assicurabili).
- Alta per il Quadrante 4 (irreversibili ma assicurabili), con funzione di utilità concava
- Bassa per il Quadrante 1 e 2 (rischi reversibili), con funzioni di utilità lineari (se siamo interessati puramente al valore atteso) o convessa (se vi è un’assimetria a nostro favore, si veda la strategia del bilanciere di Taleb per un approfondimento a riguardo).

Io mentre cerco di imitare la strategia del bilanciere di Taleb.
Cercatevi gli amici giusti
Gli ultimi rischi che vorrei affrontare sono i più soggettivi, difficilmente assicurabili e, spesso, irreversibili: quelli legati al capitale umano e alle relazioni.
Per quanto riguarda i primi, il rischio maggiore non è una perdita realizzata, ma una perdita potenziale, ossia il mancato sfruttamento di opportunità di crescita.
L’esempio più banale proviene dalla mia esperienza universitaria.
In un sistema di voti da 0 a 30 (con 18 per la sufficienza), risulta molto più utile ottenere due 23 in due esami, piuttosto che un 30 e un 17, nonostante nel primo scenario la media aritmetica sia inferiore.
- Caso : Media (il percorso universitario procede)
- Caso : Media (la bocciatura introduce un costo di fallimento elevato: tempo, impegno e stress aggiuntivi)
Il discorso si fa più complesso con le relazioni, poiché entrano in gioco emozioni e dinamiche interpersonali. Mi limito a dire che, tra tutti i rischi, terminare una relazione importante è forse l'evento più impattante, irreversibile e meno assicurabile della nostra vita.
In questo caso tuttavia, non sentendomi all’altezza di compiere una trattazione approfondita come prima, mi limito a proporre, in maniera abbastanza sbrigativa, due possibili soluzioni:
- applicare la stessa logica di prima: preferire la "minimizzazione della rovina" (evitare rotture insanabili, bugie, tradimenti… ) alla "massimizzazione della media" (avere ragione il più delle volte, stare bene assieme a tutti i costi …).
- avere amici poco permalosi
I miei, fortunatamente, non solo rientrano in questa categoria, ma (cosa più importante) mi sopportano anche quando sono di pessimo umore per il dolore al tendine. Grazie!

Se poi, oltre a sopportarmi, vengono a Zurigo a trovarmi, sono proprio quelli giusti!
Bibliografia
- Ergodicity, Luca Dellanna: il libro
- Ergodicity Economics
- Skin in the game by Taleb
- Short video explanation: ergodicity
- Very short video explanation: ergodicity
- The LoR Podcast: Che cosa è il rischio?
- The LoR Podcast: Ergodicità e Rischio (ITA)
- Too big to fail Podcast: Intervista a Luca Dellanna (ITA)
- Luca Dellanna & Mr.Rip (very old but gold)
Appendice
A.1 - Perché mio cugino si aspetta di vincere solo 0.71 gare?
Definiamo le variabili per la singola gara :
- : Mio cugino finisce la gara senza cadere
- : Mio cugino vince la gara
- : Mio cugino è sopravvissuto (non si è rotto la gamba) fino all'inizio della gara
Dal testo otteniamo:
dato che la probabilità di vincere è condizionata al fatto di essere arrivati al traguardo (evento ).
Quindi, la probabilità assoluta di vincere la gara , supponendo di essere partito (evento ), è:
Ogni volta che si presenta al cancelletto di partenza, mio cugino ha quindi il 16% di probabilità di vincere e l'80% di probabilità di poter partecipare alla gara successiva.
Inoltre, la probabilità di arrivare a partecipare alla gara (evento ) dipende dal non essere caduto in nessuna delle gare precedenti. Di conseguenza:
Possiamo quindi scrivere che la probabilità assoluta di vincere la gara (vista dall'inizio del campionato) è la probabilità di sopravvivere fino a quella gara () moltiplicata per la probabilità di vincerla una volta lì (0.16).
Il numero totale di vittorie attese, , è la somma delle probabilità di vincere ogni singola gara, da a .
che non è altro che una serie geometrica con primo termine e ragione .
A.2 - Definizioni alternative di Ergodicità?
Un evento osservabile è chiamato ergodico se il suo valore atteso è costante nel tempo e la sua media temporale converge a questo valore con probabilità uno. [Ole Peters, Alexander Adamou]
L'ergodicità è verificata se, più o meno, ogni volta che si calcola una misura statistica (nello spazio o nel tempo), si trova lo stesso risultato.
Significa che la casualità è "ben distribuita".
Un altro modo per vederla è che, quando c'è ergodicità, fare esperimenti casuali in parallelo da lo stesso risultato che fare esperimenti in serie.